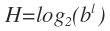(Me pregunto cómo afectará al SEO una palabra de 15 letras en el título)

Tradicionalmente, se ha venido midiendo la dificultad de las contraseñas con la entropía de Shannon. Así, el NIST define la entropía H como función de la longitud de la contraseña l y de longitud del alfabeto b, de tal forma que 

El problema de esta medida es que no recoge correctamente la dificultad de las contraseñas en el mundo real. De poco sirve este valor que solo puede ser conocido a priori ya que un posible atacante que desconozca la contraseña, también desconocerá la longitud de la misma. Por lo tanto, en la práctica, los valores b y l deben ser estimados por el atacante, afectando positivamente al valor de la entropía. Por eso prefiero diferenciar entre la entropía teórica que es la que sigue la fórmula descrita anteriormente, y la entropía práctica, que a grandes rasgos podemos asegurar que es H'≥H.

Para ilustrar esta idea voy a acudir a un famoso chiste de Dilbert.

Sin conocer los parámetros del generador de números aleatorios no podríamos calcular la entropía correctamente. La secuencia 999999 puede tener 0 bits de entropía si el RNG estuviera estropeado, 20b si consideramos que genera solo valores decimales o 39b si generase cualquier código ASCII. Desde una perspectiva estadística, un atacante debe utilizar un b̂̂, que sospecho que debería estimarse con el máximo muestral, estadístico muy ineficiente, aunque de esa afirmación no tengo prueba matemática. Llevando este último concepto al límite podemos obtener esas contraseñas de entropía inconmensurable que prometía el título.

Para ello hay que fijarse en la forma que tienen los atacantes de crackear contraseñas por fuerza bruta. Si acudimos a la documentación de Hashcat, una de las herramientas más potentes, veremos que el programa trabaja con varias "máscaras", concepto usado para referirse a subconjuntos de caracteres: ?a para minúsculas, ?d para números, ?s para símbolos, etc. Los ataques de fuerza bruta se suelen llevar a cabo utilizando ?a, que representa todos los subconjuntos y la opción -i que incrementa la longitud de la contraseña. Es decir, si nuestra contraseña es 999999, la entropía práctica para Hashcat sería de 138b ya que 

Ya nos encontramos en disposición de sintetizar nuestra contraseña de entropía inconmensurable con la ayuda de los planos astrales de unicode, estos son los planos que van del 3 al 13, espacios sin asignar en los que no hay ninguna letra todavía, pero cuya dirección existe por lo que pueden ser usados para este propósito tan bizarro. Es un espacio gigantesco, que va desde 30000 hasta DFFFF, eso son 720895 direcciones (11*2^16-1).

Para simplificar, vamos a elegir al azar uno solo de esos puntos, que podemos "imprimir" aunque al no estar asignado no se verá, con el comando echo -e "\uxxxx". Como el plano 9 está vació podemos usar la dirección \u99999 para seguir con el ejemplo hasta el absurdo infinito. Esta no-letra tiene una entropía teórica de 19.5b que para ser de un solo caracter no está mal, pero si intentamos calcular la entropía práctica nos encontramos con que Hashcat no tiene ninguna máscara que cubra ese plano astral, porque no está asignado. Hashcat no podría llegar a encontrar la contraseña original por lo que en términos coloquiales podríamos decir que la entropía práctica de \u99999 es infinita.

El concepto de infinito es muy problemático para las matemáticas y más aún para la física. No es cierto, en el sentido más estricto, que la entropía sea infinita. Es solo una forma de hablar. De hecho podemos encontrar una cifra concreta para ese "infinito", haciendo todavía más trampas porque lo que busca hashcat es el hash derivado de la función, que tiene una longitud fija y predeterminada. En el caso de Ubuntu, los hashes de las contraseñas de los usuarios están en /etc/shadow generadas con SHA512. Nuestra contraseña tendría entonces una entropía de 512b, un valor finito pero tan grande que es difícil imaginar. Por eso voy a dejar un par de enlaces tan útiles como asombrosos que nos explican la verdadera dimensión de 256b.

Desafortunadamente, el método que hemos imaginado es muy difícil y en algunos casos imposible de usar, pero es sin duda la contraseña más segura que existe.