Generador de PJs basado en 24d6

Entre las mecánicas más características de los juegos de rol clásicos y los retroclones de la que se ha venido denominando OSR, se encuentra el método para crear personajes tirando 3d6 para cada atributo, que genera una distribución N(10.5, 2.96) con un rango entre 3 y 18. Simple y efectivo… Demasiado para algunos.

Esta forma de generar PJs no tiene ningún defecto pero como es sabido, las reglas caseras son tan comunes que llegan a desplazar los pilares fundamentales del sistema d20. Y yo tengo la extraña afición de indagar en sus estadísticas para demostrar lo poco sistemáticas que son la mayor parte de ellas, como ya he hecho anteriormente.

Captcorajus lleva un canal especializado en revisiones de manuales y aventuras OSR. Veo su contenido de vez en cuando y la última vez que miré, había subido un vídeo con un título tan pretencioso como Best Character Generation Method YOU Don’t Know About, no podía perdérmelo.

El algoritmo que plantea es el siguiente:

Desde luego no es una mecánica que hubiera visto antes en ninguna parte y parecía interesante, así que no tardé en hacer unas simulaciones para analizar su funcionamiento.

Como hace bastante que no programo nada en R, he decidido pasar de mi querido Python para recordar los viejos tiempos, y escribir un pequeño script, bastante chapucero y nada funcional porque en este caso me parecía incómodo usar los *apply()

set.seed(123)
generator24d6 <- function(){
    roll <- sample(1:6, 24, replace=TRUE)
    r <- sort(roll)

    for (i in 1:6) {
        g[(i)] <- sum(r[(3 * i + 2):(3 * i + 4)])
    }
    return(g)
}
experiment <- replicate(100000, generator24d6())

palm <- hist(experiment, freq=FALSE, breaks=c(2.5:18.5),
                main="'Best' Character Generation Method YOU Don't Know About",
                xlab="", ylab="",
                xaxt = "n"
            )
axis(side=1, at=3:18, labels=3:18)

La distribución obtenida es horripilante, informe, multimodal y parece una mano ✋. Personalmente no me gusta nada. Es tan innecesariamente complicada que preferiría repartir los valores {3,6,9,12,15,18} y que cada uno los asignase al atributo que prefiera.

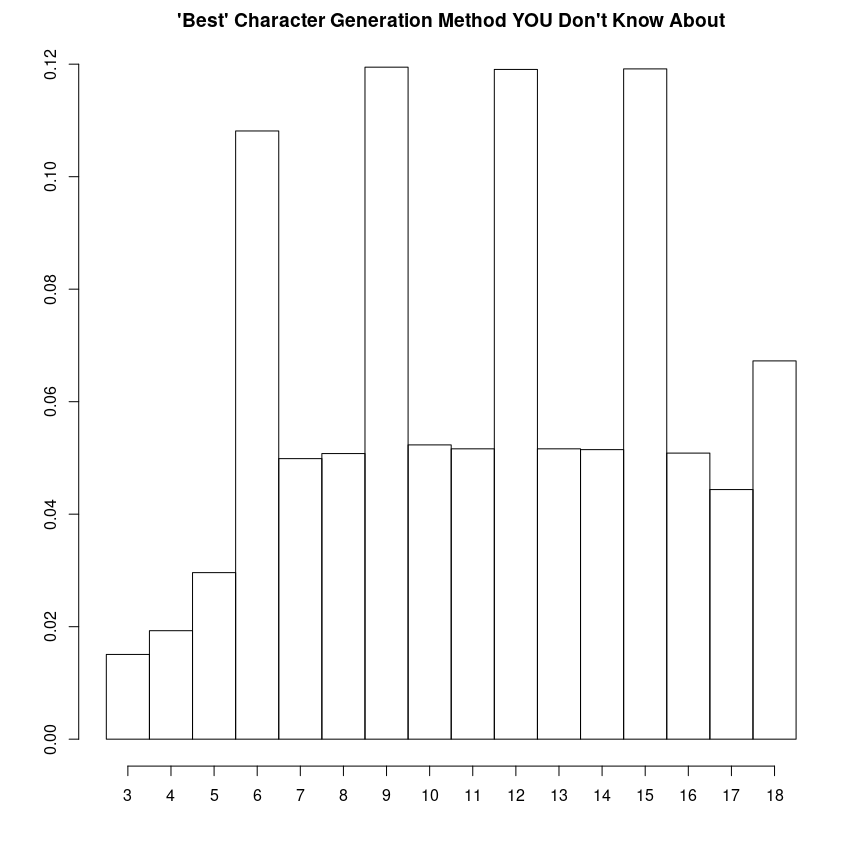
La intención del autor era que los personajes tuvieran unos atributos más variados, que no estuvieran concentrados en los mismos valores de siempre. Es decir, generar distribuciones con “colas gordas” en las que se incrementara la varianza. Aunque esto se puede hacer con dados, las mecánicas se hacen cada vez más exóticas. Personalmente, recomendaría tirar 1d10+3dF por cada atributo. Otra forma sería simular una distribución uniforme con 1d16+2 que podríamos emular con 1d4*4+1d4+2, pero teniendo ordenadores a mano, me parece un desperdicio no hacerlo de forma óptima con R

rtruncnorm(n=6, a=3, b=18, mean=10.5, sd=4)

Esta línea nos devolvería una lista con los seis atributos del juego de rol más famoso de la historia, distribuidos según una Normal con desviación típica igual a cuatro, que es aproximadamente la que se obtiene con el método este raro de los 24d6 y ligéramente menor a los 4.6 que nos daría la uniforme, que es el mayor valor posible para este rango.

La moraleja de esta historia, sin embargo, es que estas mecánicas son todas una porquería y más valdría quedarse con la original. Una de las máximas fundamentales de la OSR es que las puntuaciones de los PJs no importan tanto como la habilidad de los propios jugadores, o al menos así es como yo lo entiendo, por lo que todo este debate no tiene ningún sentido y se deberían priorizar otras facetas del juego más relevantes.