Cadenas de Markov en Hex Flores
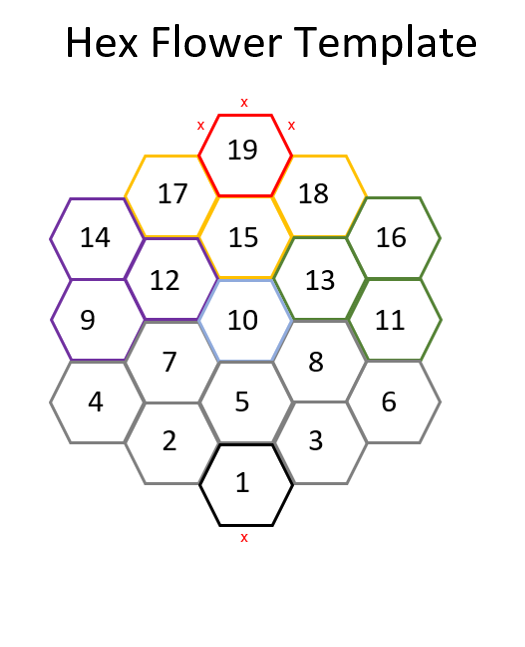
Goblin’s Henchman es el creador de una curiosa forma de generar eventos aleatorios que pueden ser usados como oráculo, autogenerador de mapas o mazmorras y cualquier cosa que se nos ocurra. En palabras del propio autor: “A versatile game engine using 2D6 and a 19-Hex Flower (it’s like a random table, but with a memory”.
Las Hex Flores son teselaciones de 19 hexágonos sobre los que nos desplazamos en función del resultado de una tirada de 2d6. Hay que aclarar que el desplazamiento no afecta a los PJs sino a una serie de eventos del juego. Se trata de una representación geométrica de una tabla aleatoria.
El autor señala que las Hex Flores tienen memoria, lo que es incorrecto. La memoria se refiere a los acontecimientos pasados mientras que estas flores evolucionan teniendo en cuenta sólo su posición actual, lo que en matemáticas hace que sean equivalentes a cadenas de Markov, modelo estocástico cuya principal característica es esta capacidad para describir eventos futuros que sólo guardan una relación de dependencia con el presente. Formalmente se expresa como
Las Hex Flores son cadenas de Markov en tiempo-homogéneo finito, irreducibles, aperiódicas y regulares. Fijándose en las probabilidades que dirigen el movimiento entre eventos podemos deducir una matriz de transición (Q). En la siguiente tabla he expresado las probabilidades multiplicadas por 36 para mayor claridad y simplicidad, en una matriz que ya es de por sí suficientemente grande.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 11 | 14 | 10 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 7 | 0 | 0 | 5 | 3 | 0 | 1 | 0 | 0 | 0 | 9 | 0 | 0 | 0 | 0 | 0 | 11 | 0 | 0 |
| 3 | 9 | 0 | 0 | 0 | 5 | 3 | 0 | 1 | 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 11 | 0 |
| 4 | 5 | 7 | 0 | 0 | 0 | 0 | 3 | 0 | 1 | 0 | 0 | 0 | 0 | 11 | 0 | 9 | 0 | 0 | 0 |
| 5 | 11 | 9 | 7 | 0 | 0 | 0 | 5 | 3 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | 3 | 0 | 9 | 0 | 0 | 0 | 0 | 5 | 0 | 0 | 1 | 0 | 0 | 7 | 0 | 11 | 0 | 0 | 0 |
| 7 | 0 | 11 | 0 | 9 | 7 | 0 | 0 | 0 | 5 | 3 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 8 | 0 | 0 | 11 | 0 | 9 | 7 | 0 | 0 | 0 | 5 | 3 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 9 | 0 | 0 | 5 | 11 | 0 | 0 | 7 | 0 | 0 | 0 | 0 | 3 | 0 | 1 | 0 | 0 | 0 | 9 | 0 |
| 10 | 0 | 0 | 0 | 0 | 11 | 0 | 9 | 7 | 0 | 0 | 0 | 5 | 3 | 0 | 1 | 0 | 0 | 0 | 0 |
| 11 | 0 | 3 | 0 | 0 | 0 | 11 | 0 | 9 | 0 | 0 | 0 | 0 | 5 | 0 | 0 | 1 | 7 | 0 | 0 |
| 12 | 0 | 0 | 0 | 0 | 0 | 0 | 11 | 0 | 9 | 7 | 0 | 0 | 0 | 5 | 3 | 0 | 1 | 0 | 0 |
| 13 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 11 | 0 | 9 | 7 | 0 | 0 | 0 | 5 | 3 | 0 | 1 | 0 |
| 14 | 0 | 0 | 0 | 1 | 0 | 5 | 0 | 0 | 11 | 0 | 0 | 7 | 0 | 0 | 0 | 0 | 3 | 0 | 9 |
| 15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 11 | 0 | 9 | 7 | 0 | 0 | 0 | 5 | 3 | 1 |
| 16 | 0 | 0 | 0 | 3 | 0 | 1 | 0 | 0 | 0 | 0 | 11 | 0 | 9 | 0 | 0 | 0 | 0 | 5 | 7 |
| 17 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5 | 11 | 0 | 9 | 7 | 0 | 0 | 0 | 3 |
| 18 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 11 | 0 | 9 | 7 | 0 | 0 | 5 |
| 19 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 11 | 0 | 9 | 7 | 9 |
Todo esto lo hago con el único propósito de encontrar un vector de estado estacionario (s) que permitiría resumir la matriz de tal forma que cada componente del vector marque la probabilidad de que se produzca el evento concreto a lo largo de toda su vida.
La Hex Flor es irreducible porque todos sus estados son recurrentes, es decir, que se puede navegar entre cualquier par de estados en un número finito de pasos porque la probabilidad entre ellos es siempre positiva. Esto implica que su comportamiento a largo plazo va a tender a una situación de equilibrio denominado estado estacionario, independiente de las condiciones iniciales de la cadena. Como existe un estado estacionario, la distribución de probabilidad marginal un movimiento después coincide con la del estado estacionario, e incluso con la del movimiento anterior porque el estado estacionario supone que la cadena sea reversible en el tiempo. Entonces sQ=s
Esto es como decir que ∞+1=∞ y ∞-1=∞ pero no hablo muy alto porque no quiero buscarme problemas con matemáticos.
Para hallar el valor de s hay que darse cuenta de que no es otra cosa que el vector propio izquierdo de la matriz Q. La ventaja de tener una matriz de 19 estados es que no hay posibilidad de calcularlo de forma algebraica y tendremos que recurrir a nuestro ordenador con R.
Q<-1/36*rbind(
c(11,14,10,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0),
c(7,0,0,5,3,0,1,0,0,0,9,0,0,0,0,0,11,0,0),
c(9,0,0,0,5,3,0,1,7,0,0,0,0,0,0,0,0,11,0),
c(5,7,0,0,0,0,3,0,1,0,0,0,0,11,0,9,0,0,0),
c(11,9,7,0,0,0,5,3,0,1,0,0,0,0,0,0,0,0,0),
c(3,0,9,0,0,0,0,5,0,0,1,0,0,7,0,11,0,0,0),
c(0,11,0,9,7,0,0,0,5,3,0,1,0,0,0,0,0,0,0),
c(0,0,11,0,9,7,0,0,0,5,3,0,1,0,0,0,0,0,0),
c(0,0,5,11,0,0,7,0,0,0,0,3,0,1,0,0,0,9,0),
c(0,0,0,0,11,0,9,7,0,0,0,5,3,0,1,0,0,0,0),
c(0,3,0,0,0,11,0,9,0,0,0,0,5,0,0,1,7,0,0),
c(0,0,0,0,0,0,11,0,9,7,0,0,0,5,3,0,1,0,0),
c(0,0,0,0,0,0,0,11,0,9,7,0,0,0,5,3,0,1,0),
c(0,0,0,1,0,5,0,0,11,0,0,7,0,0,0,0,3,0,9),
c(0,0,0,0,0,0,0,0,0,11,0,9,7,0,0,0,5,3,1),
c(0,0,0,3,0,1,0,0,0,0,11,0,9,0,0,0,0,5,7),
c(0,1,0,0,0,0,0,0,0,0,5,11,0,9,7,0,0,0,3),
c(0,0,1,0,0,0,0,0,3,0,0,0,11,0,9,7,0,0,5),
c(0,0,0,0,0,0,0,0,0,0,0,0,0,0,11,0,9,7,9)
)
Como casi todos los paquetes estadísticos, R calcula sólo el vector propio derecho, pero nosotros necesitamos el izquierdo (en operaciones matriciales no existe la propiedad conmutativa), luego tendremos que trasponer la matriz.
Además hay que normalizar el vector propio para que sus componentes sumen uno, expresando las probabilidades de cada estado en la distribución estacionaria.
s <- eigen(t(Q))$vectors
s <- s[,1]/sum(s[,1])
Con los resultados obtenidos se podría emular el comportamiento de la Hex Flor sin el tablero y sin tener en cuenta la posición actual para calcular el siguiente evento. Habría que utilizar un d100 con las DC indicadas en la tabla que recoge el vector de estado estacionario.
| hex | s | d100 |
|---|---|---|
| 1 | 0,0834 | 1 - 8 |
| 2 | 0,0765 | 9 - 16 |
| 3 | 0,0674 | 17 - 23 |
| 4 | 0,0436 | 24 - 27 |
| 5 | 0,0555 | 28 - 33 |
| 6 | 0,0386 | 34 - 37 |
| 7 | 0,0513 | 38 - 42 |
| 8 | 0,0495 | 43 - 47 |
| 9 | 0,0516 | 48 - 52 |
| 10 | 0,0495 | 53 - 57 |
| 11 | 0,0532 | 58 - 62 |
| 12 | 0,0504 | 63 - 67 |
| 13 | 0,0481 | 68 - 72 |
| 14 | 0,0433 | 73 - 76 |
| 15 | 0,0491 | 77 - 81 |
| 16 | 0,0384 | 82 - 85 |
| 17 | 0,0561 | 86 - 91 |
| 18 | 0,0524 | 92 - 96 |
| 19 | 0,0421 | 97 - 100 |
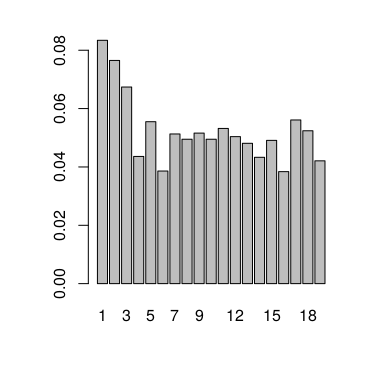
Como se ve en el histograma, la distribución estacionaria es algo irregular, con cierta exponencialidad en el sur y el resto más o menos uniforme. Toda la información generada en este post se podría resumir en el siguiente gráfico donde aparecen tanto las probabilidades de las transiciones entre eventos como las de cada uno en el estado estacionario para formar la cadena de Markov completa. En el próximo post explicaré la herramienta que utilizo para programar estos grafos y que permite automatizar y sistematizar gran parte de las complejidades relacionadas con la creación de esquemas técnicos de este tipo.
