Análisis Estadístico de Mythic: GME

El Emulador del Director de Juego de Mythic es un suplemento universal para juegos de rol que permite al game master improvisar circunstancias azarosas en las escenas de la partida para quitar peso a su intervención, lo que puede llevar a una situación de juego sin director y en ultimo término a partidas en solitario, cuya trama va surgiendo de la aleatoriedad del sistema y a la interpretación del único jugador.
El emulador de Mythic, si bien no es innovador porque recuerda a la clásica tabla universal de resultados del sistema FASERIP, ha sabido abrirse paso hasta posicionarse como una de las herramientas fundamentales para jugar en solitario a juegos de rol.

Todo el reglamento que permite adaptar este modelo a cualquier RPG se basa principalmente en una tabla del destino que actúa como oráculo para responder a preguntas binarias del jugador sobre el transcurso de la aventura. Por un lado tenemos descriptores de probabilidad, que debemos asignar a la situación objeto de consulta al oráculo. Esas posibilidades están asociadas, igualmente, a un ranking de caos, que irá variando dependiendo de la dificultad que adquiera la aventura, para equilibrar los encuentros y desafíos.
Mythic es un accesorio perfectamente jugable en su edición original, si bien un análisis en profundidad de esta tabla del destino nos muestra claramente la improvisación y desconocimiento del autor.
A cualquier persona normal le daría igual esta inconsistencia en la lógica que fundamenta el oráculo pero yo soy muy maniático y creo que puedo mejorar la mecánica de Mythic, simplificando y regularizando las estadísticas del modelo para conseguir un juego ligeramente distinto pero más elegante, matemáticamente.
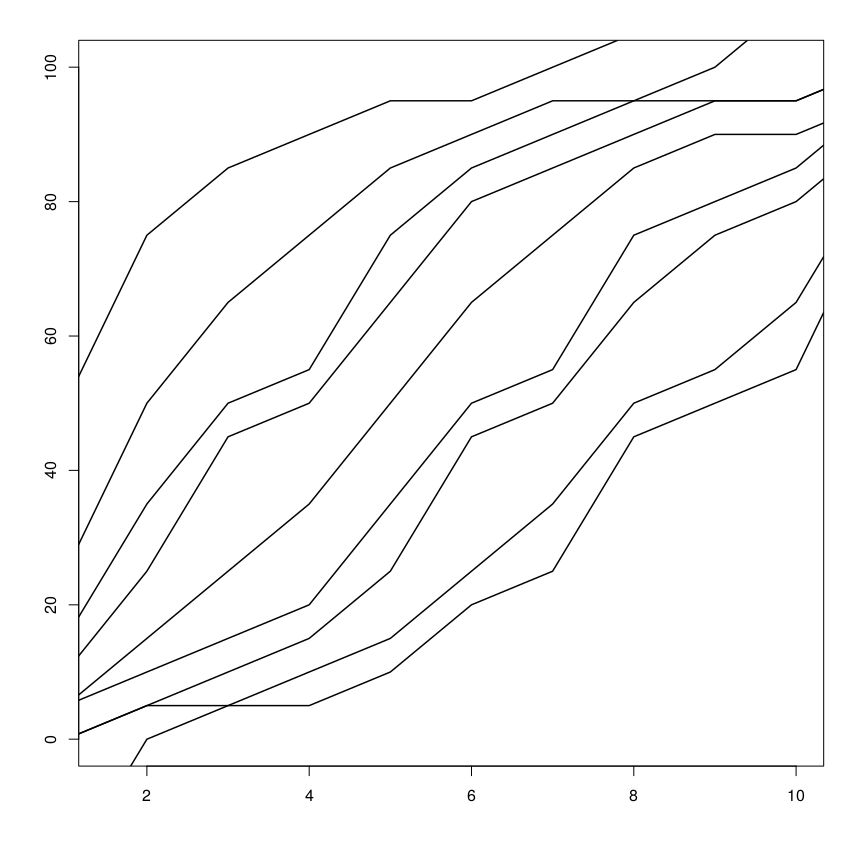
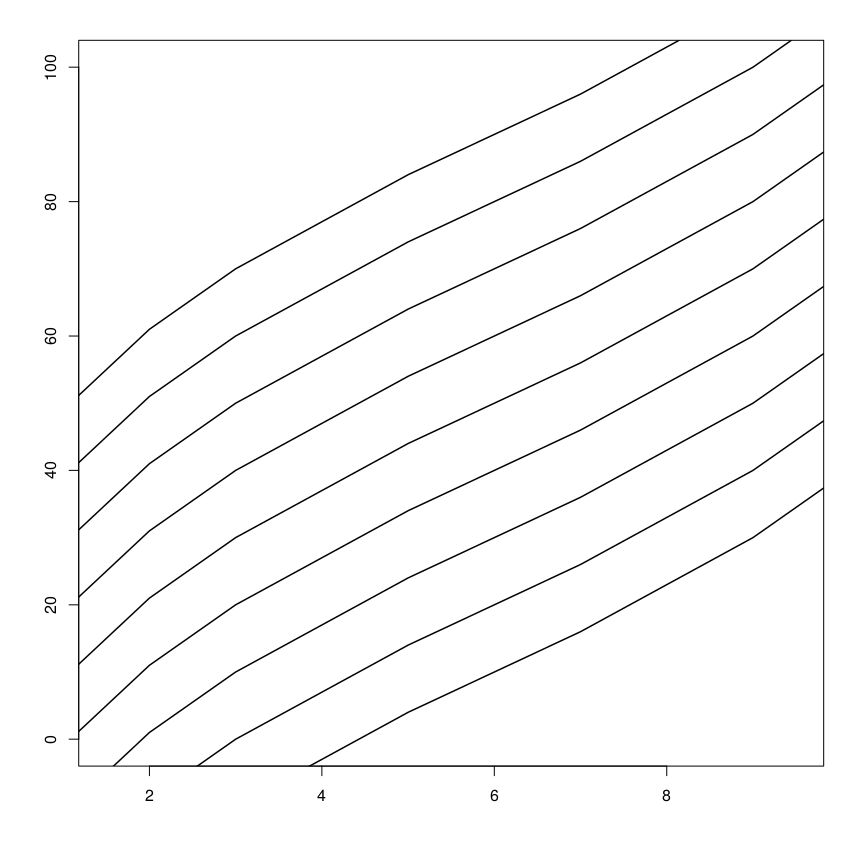
Para descomponer el sistema de juego y adentrarnos en las intenciones subyacentes del autor, vamos a hacer ingeniería inversa, buscando los fundamentos que construyen este emulador y que quizás ni siquiera el creador conociera, si surgieron de la prueba-error a través de un ajuste continuo hasta obtener los resultados deseados.
La intuición me dice que este sistema sigue una distribución de probabilidad normal. No es una hipótesis demasiado extraña ya que la mayor parte de procesos aleatorios sigue esta distribución —de ahí su nombre—. Simplemente observando el gráfico anterior podríamos confirmarlo pero para asegurar el resultado vamos a calcular el test de Shapiro para los distintos escenarios de Caos.
| Caos | Media | Desviación Típica | P-valor Shapiro |
|---|---|---|---|
| c1 | 98.18182 | 25.22625 | 0.9767736 |
| c2 | 83.63636 | 28.99059 | 0.8583959 |
| c3 | 71.81818 | 28.74654 | 0.06267893 |
| c4 | 67.27273 | 30.77041 | 0.1587115 |
| c5 | 57.27273 | 32.891 | 0.2038087 |
| c6 | 47.72727 | 32.73863 | 0.3080588 |
| c7 | 41.81818 | 32.57858 | 0.3262067 |
| c8 | 31.81818 | 28.39654 | 0.282835 |
| c9 | 25 | 29.41088 | 0.7866538 |
Como era de esperar, el oráculo es normal. Ya que estamos, voy a dibujar también los gráficos Q-Q, simplemente porque me gusta cómo quedan.
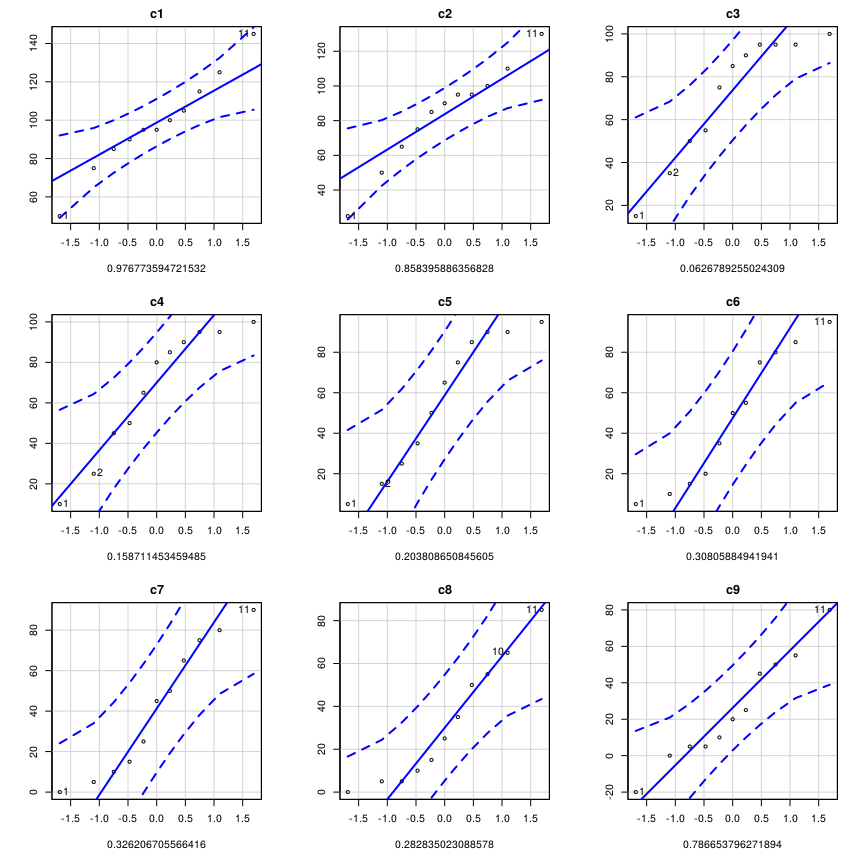
El siguiente paso es analizar la incidencia del Caos en las estadísticas. Este Caos no es el concepto que cualquiera que haya estudiado física tiene en mente. Según el autor es una variable que aumenta las probabilidades de éxito de un suceso. Habría sido mejor denominarlo suerte, fortuna, Homer Simpson aunque entiendo que el término desprende cierto carácter épico y es más comercial.
En definitiva, el Caos de Mythic es una variación en la media de las distribuciones normales que lo forman. Si seguimos profundizando vemos que esa variación es lineal, de unos 9 puntos como se aprecia de una sencilla regresión lineal. Curiosamente, la varianza de las distribuciones apenas cambia entre escenarios y se sitúa en unos 28 puntos.
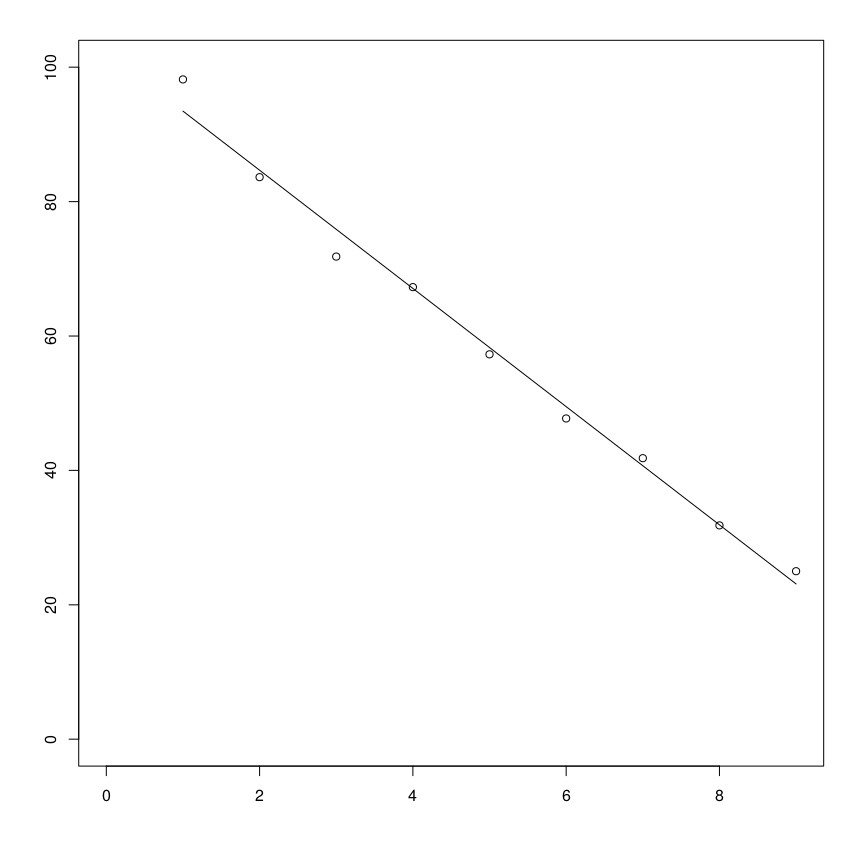
Residuals:
Min 1Q Median 3Q Max
-4.0556 -1.0328 -0.0783 1.1263 4.7172
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 102.2601 1.9182 53.31 2.14e-10 ***
seq(1, 9) -8.7955 0.3409 -25.80 3.36e-08 ***
---
Residual standard error: 2.64 on 7 degrees of freedom
Multiple R-squared: 0.9896, Adjusted R-squared: 0.9881
F-statistic: 665.8 on 1 and 7 DF, p-value: 3.358e-08
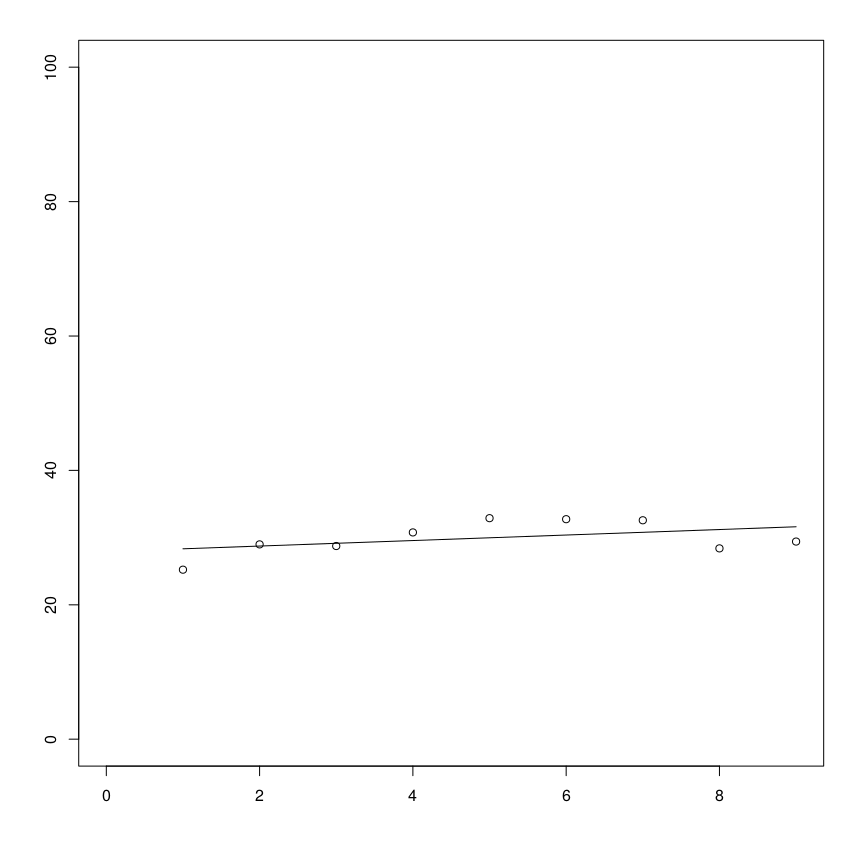
Residuals:
Min 1Q Median 3Q Max
-3.1067 -2.2005 0.2479 1.7868 2.9188
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 27.9231 1.7649 15.821 9.77e-07 ***
seq(1, 9) 0.4098 0.3136 1.307 0.233
---
Residual standard error: 2.429 on 7 degrees of freedom
Multiple R-squared: 0.1961, Adjusted R-squared: 0.08124
F-statistic: 1.707 on 1 and 7 DF, p-value: 0.2326
Finalmente, si adoptamos una hipótesis de equidistancia entre los escenarios de probabilidad —nada nos indica lo contrario— podremos reconstruir la distribución de probabilidad utilizada para formar la tabla original, aproximadamente. Sin embargo vamos a cambiar ligeramente los parámetros para obtener resultados similares en los desafíos de tirada pero que estadísticamente van a presentar ciertas características beneficiosas. Por tanto la distribución adoptada es N(10ci, 30).
Las celdas de la tabla representan los valores aleatorios, por lo que tendremos que invertir su función de probabilidad, es decir, utilizaremos la función cuantil para obtener los nuevos valores asociados a las probabilidades acumuladas equivalentes a los descriptores de probabilidad.
Aplicando la fórmula generamos la tabla corregida de Myhtic: GME.
| Chaos Rank | 5 |
|---|---|
| Impossible | 2983 |
| No way | 42185 |
| Very Unlikely | 63087 |
| Unlikely | 73788 |
| 50/50 | 94490 |
| Somewhat likely | 105091 |
| Likely | 115692 |
| Very Likely | 136394 |
| Near sure thing | 147095 |
| A sure thing | 167997 |
| Has to be | 189199 |
El efecto secundario de haber redondeado la β de la distribución de las medias a 10 es que obtenemos una variación exacta y constante entre las columnas que representan los estados de Caos. Para movernos a izquierda y derecha de la columna inicial (Caos = 5) solo hay que sumar o restar 10 —respectivamente— a los valores de cada fila. Otra ventaja de esta tabla es que ahora es simétrica en lo que se refiere a
Por lo que se podrían resumir los 99 valores de esta en media docena de números, haciendo factible su memorización. Puede llamar la atención que el 50 no corresponda con el descriptor 50/50, pero la inconsistencia se encuentra en estas últimas ya que el autor presenta unas situaciones no equilibradas, con cuatro descriptores por debajo y seis por encima. Salvo en este apartado, creo que se ha logrado una tabla más consistente para consultar como oráculo de Myhthic, respetando en todo momento la intención original del autor, pero aplicando las técnicas estadísticas adecuadas, como se puede comprobar en la gráfica final. Parece el antes y después de un anuncio de la teletienda.