Generación de Distribuciones No-Uniformes mediante el algoritmo Alias de Vose en Juegos de Rol

Hay cierto prejuicio generalizado contra los jugadores de rol que los califica como nerds pero por lo que he podido comprobar, la realidad se aleja bastante de esta idea preconcebida. La complejidad matemática de los juegos de rol es muy básica, lo que es una ventaja si uno está jugando, pero es un serio límite impuesto a los diseñadores de juegos.
El sistema d20 es uno de los más populares y está basado en el dado del mismo nombre que genera una distribución uniforme. Aunque si hay algo que caracteriza al rol es la cantidad de dados que utiliza; en este mismo sistema se hace uso del d6 para la creación de los personajes y otros eventos que requieren menos volatilidad. El uso de un solo dado, sea del valor que sea, supone la subordinación a una distribución de máxima entropía, totalmente imprevisible.
Los generadores de números aleatorios (RNG) son el pilar fundamental del rol sobre el que se construyen las estadísticas de los personajes y monstruos, encuentros y cualquier circunstancia no determinista. Un mayor control de los RNG facilitaría la tarea de diseño de juegos de rol y simplificaría los mismos, mejorando la experiencia de juego. El problema es que los diseñadores no son expertos en combinatoria y probabilidad, e históricamente han recurrido a soluciones improvisadas y basadas en prueba-error para ir refinando las mecánicas aleatorias. Los resultados son innecesariamente tediosos y no se llega a tener el control total de las distribuciones generadas.
Es aquí donde planteo mi pequeña aportación. La alternativa que ofrezco está basada en el d20 con apoyo de una tabla guía para generar resultados que siguen una distribución aleatoria determinada previamente. La ventaja de este paradigma es que se puede replicar el resultado de tiradas de cualquier dado o combinación de estos con el d20 y se pueden obtener resultados que muy difícilmente se conseguirían calcular con exóticas mezclas, para que los diseñadores de juegos y GMs vuelvan a tener un control absoluto de los procesos aleatorios que acompañan las aventuras roleras.
La forma más habitual de generar distribuciones no-uniformes a partir de uniformes es mediante el algoritmo de Box-Muller. El problema es que está diseñado para ser calculado por un ordenador, no por un dado. Es absolutamente inviable. En las asignaturas de estadística se estudia el método de la transformada inversa, bastante sencillo pero que generaría una tabla guía enorme.
Afortunadamente, profundizando en el tema, encontré un algoritmo no muy popular pero que según dicen es uno de los más elegantes e ingeniosos que existen. Se trata del algoritmo de Vose que genera tablas de tamaño n y el resultado se obtiene de forma inmediata.
Keith Schawarz publicó una extensa explicación del algoritmo y lo compara con otros métodos similares. También ofrece una implementación en Java pero como soy alérgico a este lenguaje, me he tomado la molestia de traducirlo a Python, en lo que es casi una copia línea por línea de las partes que me interesaban, si bien adaptando el algoritmo al caso del d20.
#!/usr/bin/python
from decimal import *
dice = {
"01":0,
"02":0,
"03":0.01,
"04":0.01,
"05":0.03,
"06":0.05,
"07":0.07,
"08":0.09,
"09":0.12,
"10":0.13,
"11":0.13,
"12":0.12,
"13":0.09,
"14":0.07,
"15":0.05,
"16":0.03,
"17":0.01,
"18":0.01,
"19":0,
"20":0
} #3d6
probability = {}
alias = {}
n = 20
average = 0.05
probabilities = {}
small = []
large = []
for k, v in dice.items():
probabilities[k] = Decimal(v)
if probabilities[k] >= average:
large.append(k)
else:
small.append(k)
while small and large:
less = small.pop()
more = large.pop()
probability[less] = probabilities[less] * n
alias[less] = more
probabilities[more] = (probabilities[more] + probabilities[less]) - Decimal(average)
if probabilities[more] >= average:
large.append(more)
else:
small.append(more)
while small:
probability[small.pop()] = Decimal(1)
while large:
probability[large.pop()] = Decimal(1)
Con este script podemos generar cualquier distribución de probabilidad que se nos ocurra, alterando los valores del diccionario dice. A modo de ejemplo, una típica tirada 3d6 puede ser sintetizada con este método porque sigue una distribución conocida —una N(10.5, 2.95803989) — que produce la siguiente tabla guía:
| d20 | Dificultad | Alias |
|---|---|---|
| 1 | 0 | 9 |
| 2 | 0 | 9 |
| 3 | 4 | 10 |
| 4 | 4 | 10 |
| 5 | 11 | 11 |
| 6 | 20 | 6 |
| 7 | 20 | 7 |
| 8 | 19 | 8 |
| 9 | 3 | 8 |
| 10 | 15 | 9 |
| 11 | 15 | 10 |
| 12 | 15 | 11 |
| 13 | 3 | 12 |
| 14 | 8 | 13 |
| 15 | 0 | 14 |
| 16 | 11 | 11 |
| 17 | 4 | 11 |
| 18 | 4 | 12 |
| 19 | 0 | 13 |
| 20 | 0 | 15 |
El procedimiento para utilizar esta tabla es muy sencillo
tiramos d20
nos colocamos en la fila correspondiente al resultado
tiramos d20
si superamos la dificultad de aquella fila
El resultado final es el primer d20
si no
El resultado final es el alias de esa fila
Pero este sencillo método no se conforma con síntesis tan sencillas. También es capaz de calcular la distribución de 4d6d1, muy utilizada recientemente para la creación de personajes; 4dF, la tirada de dados Fudge/Fate; incluso un humilde d6 y en realidad, cualquier distribución que se nos ocurra, ya sea simétrica o asimétrica, lineal, geométrica, campaniforme, sigmoidea, irregular o caótica.
Todo este proceso no está exento de errores. El redondeo a 1/20 impuesto por el dado provoca pequeñas divergencias respecto a la distribución original como apreciamos a continuación. Que cada cual juzgue si se encuentran en un margen de error aceptable.
| Tirada | Distribución Original | Distribución Obtenida |
|---|---|---|
| 3d6 | N(10.5, 2.958) | N(10.4525, 3.0009) |
| 4d6d1 | N(12.2446, 2.8468) | N(12.125, 3.0754) |
| 4dF | N(0, 1.633) | N(-0.03, 1.6358) |
| d6 | U(1,6) | X(3.5, 1.6903) |
A veces una imagen vale más que mil palabras, así que he elaborado los siguientes gráficos de las distribuciones anteriormente tratadas, obviando el hecho de que son generalizaciones de los verdaderos resultados y que las originales son discretas. Se muestra la PDF original en línea discontinua para que contraste con la estimación verdaderamente obtenida.
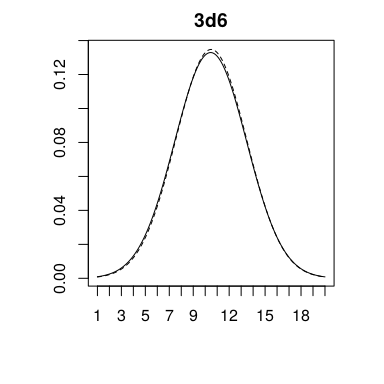
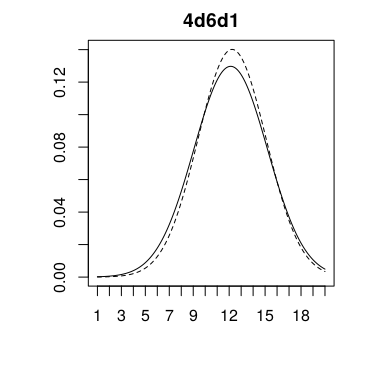
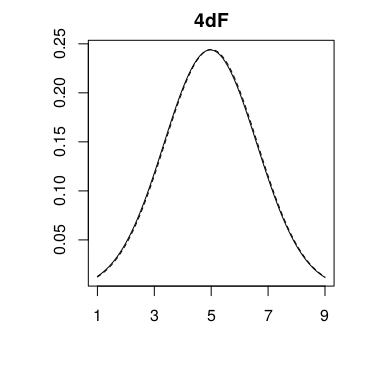
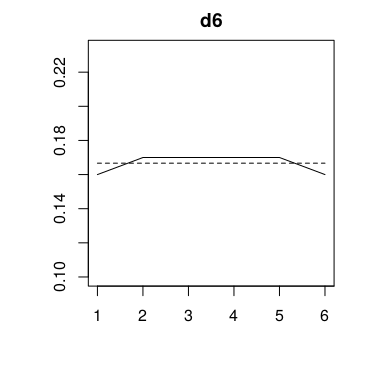
Finalmente y a modo de conclusión se recoge en la siguiente tabla las tiradas de dificultad (D) y alias (A) para los casos tratados. Esta es la única que necesitamos para jugar.
| d20 | s3d6 D | s3d6 A | s4d6d1 D | s4d6d1 A | s4df D | s4df A | sd6 D | sd6 A |
|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 9 | 0 | 12 | 4 | 6 | 4 | 3 |
| 2 | 0 | 8 | 0 | 13 | 20 | 0 | 20 | 0 |
| 3 | 4 | 9 | 4 | 9 | 16 | 2 | 12 | 2 |
| 4 | 4 | 12 | 4 | 14 | 12 | 7 | 16 | 6 |
| 5 | 11 | 12 | 4 | 11 | 12 | 4 | 8 | 4 |
| 6 | 12 | 13 | 8 | 12 | 8 | 3 | 0 | 1 |
| 7 | 12 | 6 | 11 | 12 | 4 | 6 | 0 | 2 |
| 8 | 4 | 7 | 16 | 15 | 0 | 5 | 0 | 1 |
| 9 | 8 | 8 | 8 | 13 | 4 | 7 | 0 | 1 |
| 10 | 8 | 15 | 11 | 15 | 0 | 8 | 0 | 5 |
| 11 | 4 | 14 | 4 | 14 | 0 | 5 | 0 | 5 |
| 12 | 16 | 9 | 8 | 16 | 0 | 4 | 0 | 6 |
| 13 | 20 | 0 | 20 | 0 | 0 | 3 | 0 | 2 |
| 14 | 12 | 12 | 16 | 12 | 0 | 5 | 0 | 4 |
| 15 | 8 | 11 | 16 | 11 | 0 | 5 | 0 | 5 |
| 16 | 11 | 10 | 16 | 9 | 0 | 4 | 0 | 6 |
| 17 | 4 | 10 | 16 | 10 | 0 | 4 | 0 | 4 |
| 18 | 4 | 11 | 8 | 15 | 0 | 6 | 0 | 3 |
| 19 | 0 | 11 | 0 | 11 | 0 | 6 | 0 | 3 |
| 20 | 0 | 10 | 0 | 10 | 0 | 7 | 0 | 6 |
P.S. Para calcular las probabilidades de la suma de los valores de los dados, se ha utilizado la intimidante fórmula
